Pour que l’on puisse voir un objet, il faut réunir certaines conditions, notamment que l’œil «détecte» la présence de l’objet.

Ceci entraîne l’arrivée de la lumière provenant de l’objet dans l’œil. Il faut donc, dans un premier temps, que l’objet émette de la lumière. Cette lumière pourrait être produite par l’objet, et dans ce cas-là l’objet est une source primaire de lumière (objet lumineux) ; ou la lumière pourrait être diffusée par l’objet, et dans ce cas l’objet est une source secondaire de lumière (objet éclairé).

Mais dans un deuxième temps, il faut des conditions propices au passage de la lumière de l’objet vers l’œil humain, c’est-à-dire des conditions nécessaires pour la propagation de la lumière.

Une source lumineuse ponctuelle émet de la lumière dans tous les sens. L’ensemble des rayons lumineux qui pénètrent dans l’œil forment un faisceau lumineux. Quand la source lumineuse s’éloigne, l’angle du faisceau lumineux se rapproche de 0. Pour un objet situé très loin, on dit qu’il se situe « à l’infini », et les rayons pénétrant l’œil sont considérés comme parallèles.

De manière générale une lentille (= lens) est un système optique qui sert à dévier et à déformer un faisceau(= beam) de lumière. La lentille la plus simple est un objet transparent avec une surface courbée. Elles le fait grâce à la réfraction du faisceau lumineux pendant l’entrée (et souvent la sortie) du faisceau dans le système optique. Comme nous allons voir par la suite, il y a différentes catégories de lentilles. Celles qui nous intéressent et que l’on va étudier sont des lentilles minces.

Les lentilles minces sont caractérisées par :

• Centre optique (O) : le point particulier où un rayon incident n’est pas dévié.

• Foyer image (`F’`) (= focal point): le point de convergence des rayons lumineux arrivant de l’infini (i.e. parallèles).

• Plan focal image (= focal plane): on appelle plan focal image le plan perpendiculaire à l’axe optique passant par le foyer image `F'`.

• Foyer objet (`F`) : le point dont l’image se trouve à l’infini après avoir traversé la lentille. Il est situé à la même distance que le foyer image, par rapport au centre optique, mais de l’autre côté de la lentille.

• Plan focal objet : on appelle plan focal objet le plan perpendiculaire à l’axe optique passant par le foyer objet `F`.

• Distance focale (`f’`) (= focal length): la distance entre le foyer image et le centre optique. (`\overline{OF'}=f'`) et (`\overline{OF}=f`).

• Vergence (C) : Inverse de la distance focale. `C=\dfrac{1}{f'}` . La vergence s’exprime en « dioptries » dont le symbole est `\delta` (quand `f'` est exprimé en mètres).

Mettons en place maintenant les règles pour la construction graphique de l’image d’un objet donnée par une lentille mince. En général si on prend un point B sur l’objet, on peut trouver son image en suivant les règles suivantes :

• Un rayon lumineux passant par `O` n’est jamais dévié.

• Un rayon arrivant, qui est parallèle à l’axe optique, émerge en passant par le foyer image `F'`.

Les lentilles minces convergente et divergente sont identiques avec la seule différence étant l’inversion des foyers objets et image: dans une lentille convergente le foyer image se situe après le centre optique, tandis que pour une lentille divergente le foyer image se situe avant le centre optique (cf. 4 )

Nous représentons normalement un objet par une flèche verticale (`AB`), perpendiculaire à l’axe optique. En traçant au moins deux de ces trois rayons, le point `B’` (image du point `B`) est situé à l’intersection des rayons émergents, comme détaillé dans les figures suivantes :

Exemple:

Remarque. Construction d’image pour une lentille divergente

L’image qui se forme, à travers un système optique, peut être soit réelle, soit virtuelle.

Exemple:

Faisons quelques applications de ces règle afin de mieux les intégrer.

\dfrac{1}{\overline{OA'}} - \dfrac{1}{\overline{OA}} = \dfrac{1}{\overline{f'}}

Exemple:

D’abord nous construisons l’image de `AB` selon les règles que nous avons déjà vues.

En suite afin de déterminer le grandissement il faut mesurer la taille de `AB` ainsi que celle de `A'B'`, et puis calculer leur rapport.

D’après l’échelle établie par le graphe `\overline{A'B'} = -2,0 \; cm` et `\overline{AB} = 1,0 \; cm`.

\begin{aligned}
    \gamma &=  \dfrac{\overline{A'B'}}{\overline{AB}} \\ &= \dfrac{-2,0}{1,0} \\ &= -2,0 
\end{aligned}

Faisons donc quelques remarques d’après les résultats précédents :

• les grandeurs `\overline{A'B'}` ou `\overline{AB}` sont des grandeurs orientées, et donc il faut respecter leurs orientations physique en leur attribuant le bon signe `-/+`.

• Le signe de `\gamma` signifie si l’image est dans le même sens que l’objet (`\gamma>0`) ou renversée (`\gamma<0`).

• La norme du grandissement `\abs{\gamma}` signifie le facteur de grandissement.

• L’image est plus grande si `\abs{\gamma}>1` et plus petite si `\abs{\gamma}<1`.

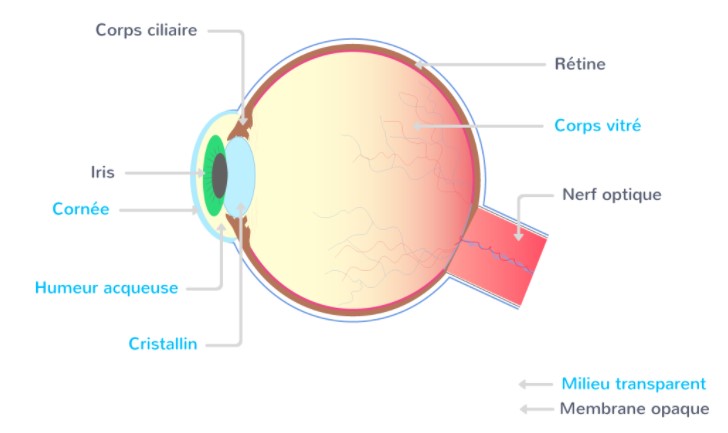
Nous avons maintenant tous les outils nécessaires pour la modélisation de l’œil. Même si, physiologiquement, la structure de l’œil paraît assez complexe, physiquement son fonctionnement est basé sur quelques principes physiques simples et facilement modélisables. L’œil est constitué d’une lentille qui modifie le trajet de la lumière pénétrant dans l’œil (le cristallin(= lens)) et d’un capteur de lumière situé derrière la lentille (la rétine(= retina)) (cf. Figure ci-contre).

Ce modèle s’appelle l’œil réduit, car on remplace l’ensemble des milieux transparents (humeur aqueuse, cristallin) par une lentille mince convergente. Il s’agit donc de l’association d’un diaphragme accolé à une lentille convergente, et un écran où se forme l’image projetée par la lentille.

Dans notre modélisation, la rétine sera remplacée par un écran, où se forment les images des objets dont la lumière pénètre l’œil. La distance entre la lentille et l’écran est de `17mm` afin de bien modéliser la taille réelle de l’œil humain.

L’œil humain est soit dans un état de repos (les muscles ciliaires ne sont pas contractés), ou dans un état d’accommodation (muscles ciliaires contractés). Dans son état de repos, le foyer image de l’œil est situé sur la rétine, c’est-à-dire la lumière provenant d’un objet situé à l’infini converge sur la rétine sans action musculaire de la part de l’œil. Par conséquent si l’objet se rapproche de l’œil, sans accommodation, son image se forme, théoriquement, en arrière de la rétine.

Les muscles ciliaires, en se contractant, changent la distance focale de la lentille, rapprochant le foyer image jusqu’à ce que l’image se forme parfaitement sur la rétine : c’est l’accommodation (cf. Figure 6).

La différence principale, bien sûr, entre cette modélisation et l’œil, est que la distance focale de la lentille dans notre modèle est fixe, alors que l’œil est capable, grâce à l’action des muscles ciliaires de changer sa distance focale (i.e. accommodation). On peut remédier à ce problème en changeant la lentille pour des différents objets en fonction de leurs distances par rapport à l’œil.

La quasi-totalité des êtres humains sont nés avec des yeux qui fonctionnent correctement dans la première partie de la vie. Mais à partir d’un certain âge, des défauts de vision peuvent se produire ; ce que l’on corrige grâce aux lunettes. Par ailleurs, la cause de ces défauts est souvent la déformation de l’œil en raison de la croissance. C’est pourquoi la période de puberté est le début de l’apparition de ces problèmes pour beaucoup. La croissance du crâne qui entraîne une légère déformation du globe de l’œil qui a pour résultat le décalage de la rétine par rapport au point focal du cristallin.

Nous allons donc comprendre le principe des défauts oculaires, en les étudiant avec notre modèle de l’œil réduit.

Dans chaque défaut, l’image de l’objet ne se forme pas sur la rétine, et donc l’image vue est floue. Si on y pense, on voit bien deux possibilités :

• L’image se forme devant la rétine, donc l’œil est trop convergent : l’œil est myope.

• L’image se forme derrière la rétine, donc l’œil n’est pas suffisamment convergent : l’œil est hypermétrope (ou presbyte).

Afin de corriger ce défaut, il faut repousser la convergence vers la rétine, c’est à dire rendre l’œil moins convergent. Ceci est corrigé en plaçant une lentille divergente devant les yeux : des lunettes divergentes ! Le choix de la puissance des lunettes dépend du degré de myopie.

Afin de corriger ce défaut il faut faire revenir le foyer image de l’œil sur la rétine, c’est-à-dire rendre l’œil plus convergent. Ceci est corrigé en plaçant une lentille convergente devant les yeux : des lunettes convergentes ! Comme avant, le choix de la puissance des lunettes dépend du degré d’hypermétropie.

La presbytie n’est pas vraiment une maladie comme la myopie ou l’hypermétropie, c’est plutôt une conséquence du vieillissement de l’œil. Il s’agit du durcissement du cristallin qui rend l’accommodation plus difficile pour l’œil. Le résultat est l’apparition de difficultés de vision aux distances proches. D’où le besoin de lunettes correctives pour la lecture. En ce sens-là les symptômes ressemblent beaucoup à ceux de l’hypermétropie. Par conséquent, la correction, comme pour l’œil hypermétrope, s’effectue grâce aux lentilles convergentes.