La lumière étant une onde électromagnétique (= electromagnetic wave), elle ne nécessite pas de milieu matériel pour sa propagation (chapitre précédent). Cependant, ceci ne veut pas dire que la lumière ne peut pas passer dans un milieu matériel. En fait, tant que le milieu est transparent et non opaque, la lumière peut s’y propager (sinon comment la lumière peut-elle traverse une vitre, ou l’atmosphère).

Nous avons vu aussi que la célérité (= phase velocity) de la lumière est notée `c=3,0\cdot 10^{8}\; m\cdot s^{-1}`, et que cette vitesse est la vitesse limite dans l’univers (merci Albert !). Mais, la célérité de la lumière n’est pas constante, c’est-à-dire que la lumière se propage à des vitesses plus lentes dans différents milieux transparents. Sans entrer dans les détails, en raison des interactions entre la lumière - en tant qu’onde électromagnétique - et les champs électromagnétiques présents dans les atomes et les molécules, la lumière se déplace plus lentement dans un milieu matériel. Parmi les facteurs influençant la célérité de la lumière dans un milieu matériel, nous pouvons compter la densité du milieu comme un facteur important.

Nous caractérisons la célérité de la lumière dans un milieu matériel en définissant un indice de réfraction du milieu.

En se basant sur cette définition, nous pouvons faire quelques conclusions simples :

• `n` est une grandeur sans unité (= unitless),

• dans le vide l’indice de réfraction est `n=1` ,

• de manière générale `n\geq1` ,

• plus `n` est important, plus la lumière se déplace lentement dans le milieu concerné.

• plus `n` est important, plus le milieu est dit réfringent.

Voici un tableau de quelques indices de réfraction communs :

Les lois de Descartes-Snell nous donnent, de manière quantitative, des relations mathématiques qui nous permettront de déterminer le comportement d’un rayon lumineux incident à une surface, avant et après son incidence.

Ils parlent notamment de deux phénomènes : la réflexion et la réfraction. Il faut donc d’abord définir quelques termes importants.

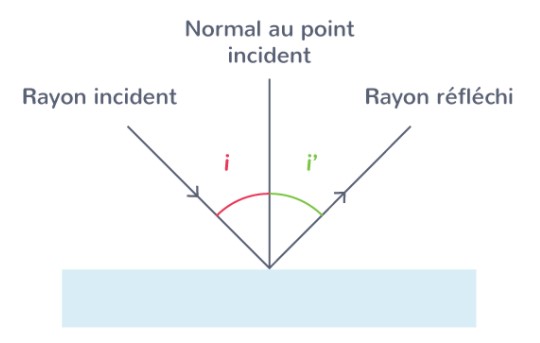
En optique, une réflexion est le renvoie d’un rayon lumineux par une surface. L’angle qui se forme entre le rayon réfléchi et la normale au point d’incidence s’appelle l’angle de réflexion noté `i'` (ou `r`).

Dans le cas d’une réflexion d’après la loi de Descartes-Snell pour la réflexion, l’angle de réflexion et l’angle d’incidence ont la même valeur :

i = i'\text{\quad ou \quad } i = r

C’est un résultat presque évident, car nous le voyons tout le temps dans le quotidien. Mais il est important de l’énoncer, et la démonstration de ce résultat, par un raisonnement théorique, est au-delà du niveau de seconde.

D’abord définissons quelques termes pour mieux comprendre la figure 2:

• Le rayon lumineux qui arrive sur le dioptre s’appelle le rayon d’incidence.

• Le point du dioptre traversé par le rayon incident s’appelle le point d’incidence (`I`).

• Le rayon lumineux qui se propage dans le deuxième milieu après la réfraction s’appelle le rayon réfracté.

• La droite perpendiculaire au point d’incidence `I` s’appelle la normale à la surface de séparation.

• L’angle entre le rayon d’incidence et la normale s’appelle l’angle d’incidence `i` .

• L’angle entre le rayon réfracté et la normale s’appelle l’angle de réfraction `r`.

• Le plan contenant le rayon incident et la normale au point d’incidence s’appelle le plan d’incidence.

Cette loi assure que le phénomène de réfraction reste en deux dimensions, i.e. dans un plan, celui du rayon incident.

n_1\cdot \sin{i} = n_2\cdot \sin{r}

n_1 \sin{i} = n_2 \sin{r}

\begin{aligned}
   n_1 \sin{i} &= n_2 \sin{r} \\     
   \sin{r} &= \left( \dfrac{n_1}{n_2} \right)\cdot\sin{i} \\
   r &= \arcsin{\left[\left( \dfrac{n_1}{n_2} \right)\cdot \sin{i} \right]}
\end{aligned}

\begin{aligned}
    r &= \arcsin{\left[\left( \dfrac{n_1}{n_2} \right)\cdot \sin{i} \right]} \\
    &= \arcsin{\left[\left( \dfrac{1,00}{1,512} \right)\cdot \sin{60} \right]} \\
    &= 35\degree
\end{aligned}

Enfin, nous pouvons mieux expliquer le phénomène de la dispersion de la lumière blanche. En fait, la dispersion de la lumière blanche n’est que sa réfraction (ou plutôt double réfraction) dans le prisme (ou n’importe quel autre milieu).

Le point clef à comprendre est le fait que l’indice de réfraction est légèrement différent selon la couleur (et donc la longueur d’onde) de la lumière colorée (oui, cela implique que les lumières de différentes couleur n’ont pas la même célérité dans un même milieu de propagation! ).

Par conséquent pour un même angle d’incidence `i`, l’angle de réfraction `r` est légèrement différent pour chaque lumière colorée : les différentes lumières colorées constituant la lumière blanche subissent un angle de réfraction différemment, les séparant à la sortie du prisme.

En passant à travers d’un prisme en verre (ou plexiglas) la lumière franchit deux dioptres : air/verre et puis verre/air. Puisqu’un prisme réfracte différemment les radiations qui composent la lumière blanche, cela signifie que l’indice du verre n’a pas la même valeur selon les longueurs d’onde de ces radiations.

Pour le moment nous avons vu des exemples de réfraction où nous passons d’un milieu moins réfringent vers un milieu plus réfringent (i.e. avec un indice `n` plus petit vers un indice plus grand). C’est le cas d’un passage de l’air (`n\sim 1,00`) dans le verre (`n\sim 1,50`). Voyons (dans les figures suivantes) l’évolution de l’angle de réfraction pendant le passage d’un rayon incident perpendiculaire vers un rayon incident presque parallèle à la surface de séparation.

Ce qui est important à noter est le fait que à tout moment `i > r`. Par conséquent, même avec un rayon incident presque parallèle à la surface de séparation le rayon réfracté reste dans le deuxième milieu, et avec une valeur bien inférieure à l’angle du rayon incident.

Posons-nous la question de ce qui se passerait dans le cas inverse : si la lumière passe du verre dans l’air (la différence étant que le passage est d’un milieu avec un indice de réfraction supérieur vers un milieu avec un indice de réfraction inférieur), que se passe-t-il?.

Nous voyons clairement une différence fondamentale par rapport au cas précédent : l’angle de réfraction `r > i`. Par conséquent, l’angle de réfraction croît plus rapidement que l’angle d’incidence et donc nous arrivons, à un moment donné, à un angle d’incidence pour lequel l’angle de réfraction est presque `90\degree`. Si l’on dépasse cet angle critique, il n’y aura plus de réfraction! Ce phénomène s’appelle une réflexion totale, ou une réflexion interne.

Une compréhension de la réfraction, et surtout de la notion de la réflexion totale interne, nous permet aussi d’expliquer de nombreux autres phénomènes. Voici en quelques-uns :

Le phénomène d’arc-en-ciel est comme la dispersion de la lumière blanche dans un prisme, cette fois dans une goutte d’eau à la place du prisme, comme vous le voyez dans la figure ci-après.

La lumière venant du soleil traverse un premier dioptre en entrant la goutte d’eau. Elle subit une première réfraction et donc une première séparation des lumière colorée. Puis, après une réflexion interne (que l’on va étudier dans la partie suivante), elle traverse une deuxième fois un dioptre (cette fois eau-air) et subit une deuxième réfraction, séparant davantage les lumières colorées, comme dans un prisme.

A sa sortie, la lumière blanche a bien été dispersée et décomposée en lumières colorées. Un point intéressant à noter est que pour qu’un arc-en-ciel soit visible, il faut que l’observateur soit situé entre le soleil (dans son dos) et la pluie (devant lui).

Un mirage est une déviation forte des rayons du soleil, en raison de la création d’un milieu hétérogène dû à une variation forte de la température de l’air à proximité du sol.

Dans certaines conditions, notamment quand le sol est très chaud en raison d’un fort ensoleillement, l’air voisin du sol est bien plus chaud que l’air plus haut. En effet, plus on s’éloigne du sol moins l’air serait chaud. Un changement de température d’air entraîne un changement de sa densité, et par conséquent son indice de réfraction (moins dense `\longrightarrow` moins réfringent).

Les rayons lumineux venant du ciel vont donc subir des réfractions successives jusqu’au niveau du sol, où ils subiront une réflexion totale, et seront renvoyés vers le haut. Si l’on reçoit ces rayons, nous aurions l’impression de voir une flaque d’eau au niveau du sol, mais c’est simplement la réflexion du bleu du ciel dans le sol.

Une fibre optique est une fibre en verre ou en plastique (très fin) qui, grâce au phénomène de réflexion totale permet la conduction d’un rayon lumineux.

Ce coeur de la fibre est entouré d’une gaine avec un indice de réfraction inférieur, ce qui permet la réflexion totale de la lumière, comme visible dans la figure ci-après.

Une fibre optique a des avantages importants par rapport à un câble électrique, notamment par le fait de pouvoir transmettre l’information à la vitesse de la lumière.