# Energie de changement d'état

# Énergie de changement d’état

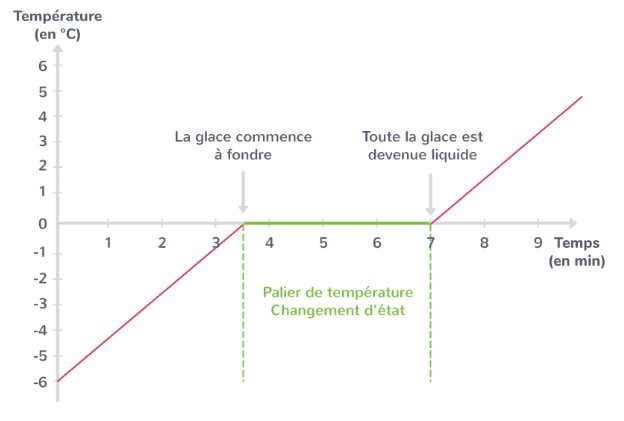
Evolution de la tempréature d'une glaçon en fonction du temps, lors d'une fusion

Vous Souvenez-vous de l’expérience de la fonte d’un glaçon en cinquième? Vous aviez suivi la température d’un glaçon lors de sa fusion. La figure3 représente l’évolution de la température du glaçon lors de sa fusion. Nous observons un palier très caractéristique à la température de fusion. L’interprétation de ce palier est : au début du palier il y a de l’eau solide à 0\degree et à la fin du palier il y a de l’eau liquide à 0\degree.

Conclusion : l’eau à l’état liquide a plus d’énergie que l’eau à la même température à l’état solide.

Ce palier représente l’énergie de changement d’état, c’est à dire la quantité d’énergie transférée pour que le corps change d’état (ici de solide en liquide). Cependant, le plus souvent, l’énergie de changement d’état est exprimée en terme d’énergie massique de changement d’état

success**Définition : *Énergie massique de changement d’état

(= latent heat)***

C’est la quantité d’énergie nécessaire pour un changement d’état de 1\; kg d’un corps.
Elle est notée E_{\text{changement d'état}}, et s’exprime en J\cdot kg^{-1}
Elle peut être appelée aussi :
- Chaleur latente, notée L_{\text{changement d'état}}
- Enthalpie de changement d’état, notée \Delta H_{\text{changement d'état}}
Elle est notée positive si la transformation est endothermique (car le transfert thermique s’effectue du milieu vers le corps, entrant dans le corps alors).
Elle est notée négative si la transformation est exothermique (car le transfert thermique s’effectue du corps vers le milieu, quittant le corps alors).

Exemple:

Pour l’eau E_{\text{solidification}} = - 3,33\cdot 10^{5}\; J\cdot kg^{-1}
E_{\text{fusion}} > 0
E_{\text{solidification}} < 0
E_{\text{solidification}} = - E_{\text{fusion}}

Pour finir, il est important de faire la distinction donc entre l’énergie de changement d’état et l’énergie massique de changement d’état. La première est la quantité totale d’énergie transférée pour faire la transformation (dépendant donc de la quantité de matière à transformer), tandis que la seconde est une caractéristique de la substance, c’est à dire une propriété de la matière (et indépendante de la masse).

Il existe donc une relation très simple entre l’énergie de changement d’état noté Q, et l’énergie massique de changement d’état L : $$Q = m\cdot L $$

\triangleright \quad Exerice. Déterminer l’énergie nécessaire pour faire fondre 250\; g de glace. (Donnée : L_{\text{fusion}}(eau) = 3,33\cdot 10^{5}\; J\cdot kg^{-1}